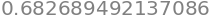.ipynb .pdf

repository open issue suggest edit

Binder Colab

Contents

The Gaussian (Normal) Distribution

Probability Distribution Function

The Normal (Gaussian) distribution probability distribution function is

\[ f\left(x; \mu, \sigma\right) = \frac{1}{\sqrt{2\pi}\sigma}\,e^{-\left(x-\mu\right)^2/2\sigma^2}, \]

normalized to unity,

\[ \int\limits_{-\infty}^{\infty} f\left(x; \mu,\sigma\right)\,dx = 1, \]

is symmetrically distributed about its mean, \(\mu\), with width \(\sigma\).

Full Width at Half Maximum (FWHM)

The full width at half maximum (FWHM) is the distance between points on a curve at which the function reaches half its maximum value. The FWHM is often used to describe the “width” of a distribution.

For a 1-dimensional Gaussian, it is seen that as the maximum value occurs as \(x = \mu\) (by definition), half of the maximum value is

\[\begin{split} \begin{align*} \left.\frac{1}{\sqrt{2\pi}\sigma}\,e^{-\left(x-\mu\right)^2/2\sigma^2}\right|_{x = x \text{ of (max/2)}} &= \frac{1}{2} f\left(x_{\text{max}}\right)\\ &= \frac{1}{2} f\left(\mu\right) = \frac{1}{2} \frac{1}{\sqrt{2\pi}\sigma}, \end{align*} \end{split}\]

resulting in the equality

\[ e^{-\left(x-\mu\right)^2/2\sigma^2} = \frac{1}{2}, \]

which is (taking the log)

\[ -\frac{\left(x-\mu\right)^2}{2\sigma^2} = -\ln2. \]

Thus, solving the equality,

\[ \left(x-\mu\right)^2 = 2\sigma^2 \ln2, \]

yields

\[ x_{\pm} = \pm \sigma \sqrt{2 \ln 2} + \mu. \]

Thus, the FWHM is

\[\begin{split} \begin{align*} \text{FWHM} &= x_{+} - x_{-}\\ &= \left(\sigma \sqrt{2 \ln 2} + \mu\right) - \left(-\sigma \sqrt{2 \ln 2} + \mu\right)\\ &= \boxed{2\sqrt{2\ln2}\sigma}\,. \end{align*} \end{split}\]

N.B.: It is seen that the FWHM for a Gaussian is independent of both the normalization constant and the mean, and is only dependent on the standard devaiation of the Gaussian.

Probability and the Error Function

The probability that a Normally distributed random variable will lie in a range of values symmetrically integrated over is given by

\[\begin{split} \begin{align*} \text{Pr}\left(\mu - y \leq x \leq \mu + y\right) &= \int\limits_{\mu - y}^{\mu + y}\frac{1}{\sqrt{2\pi}\sigma}\,e^{-\left(x-\mu\right)^2/2\sigma^2}\,dx\\ &= \int\limits_{\mu}^{\mu + y}\frac{2}{\sqrt{2\pi}\sigma}\,e^{-\left(x-\mu\right)^2/2\sigma^2}\,dx. \end{align*} \end{split}\]

Making the substitution

\[ t = \frac{\left(x-\mu\right)}{\sqrt{2}\sigma}, \]

then

\[\begin{split} \begin{align*} \text{Pr}\left(\mu - y \leq x \leq \mu + y\right) &= \int\limits_{\mu}^{\mu + y}\frac{2}{\sqrt{2\pi}\sigma}\,e^{-\left(x-\mu\right)^2/2\sigma^2}\,dx\\ &= \boxed{\frac{2}{\sqrt{\pi}} \int\limits_{0}^{y/\sqrt{2}\sigma}e^{-t^2}\,dt \equiv \text{erf}\left(\frac{y}{\sqrt{2}\sigma}\right)}\,. \end{align*} \end{split}\]

Cumulative Distribution Function (cdf)

For the cumulative distribution function (cdf),

\[ \Phi\left(x\right) = \int\limits_{-\infty}^{x}f\left(t;\mu,\sigma\right)\,dt, \]

it is seen, noting from the form of the error function, that

\[ \begin{equation*} \frac{2}{\sqrt{\pi}} \int\limits_{0}^{y/\sqrt{2}\sigma}e^{-t^2}\,dt = \frac{2}{\sqrt{2 \pi}} \int\limits_{0}^{y/\sigma}e^{-t^2/2}\,dt = \text{erf}\left(\frac{y}{\sqrt{2}\sigma}\right), \end{equation*} \]

import sympy as sym

sym.init_printing(use_unicode=True, wrap_line=False, no_global=True)
from sympy.abc import sigma

(
    t,
    y,
) = sym.symbols("t y")
sym.integrate(
    (2 / sym.sqrt(sym.pi)) * sym.exp(-(t ** 2)), (t, 0, y / (sym.sqrt(2) * sigma))
)

sym.integrate((2 / sym.sqrt(2 * sym.pi)) * sym.exp(-(t ** 2) / 2), (t, 0, y / sigma))

then for the standard Gaussian (\(\mu = 0\), \(\sigma=1\))

\[\begin{split} \begin{align*} \Phi\left(x\right) &= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{x} e^{-t^2/2}\,dt\\ &= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{0} e^{-t^2/2}\,dt + \frac{1}{\sqrt{2\pi}}\int\limits_{0}^{x} e^{-t^2/2}\,dt\\ &= \frac{1}{2} + \frac{1}{2} \text{erf}\left(\frac{x}{\sqrt{2}}\right)\\ &= \frac{1}{2} \left(1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right) \end{align*} \end{split}\]

so it is likewise seen that

\[\begin{split} \begin{align*} \text{Pr}\left(\mu - n \sigma \leq x \leq \mu + n\sigma\right) &= \Phi(n) - \Phi(-n)\\ &= \Phi(n) - \left(1-\Phi(n)\right)\\ &= \frac{1}{2} \left(1 + \text{erf}\left(\frac{n}{\sqrt{2}}\right)\right) - \left[1-\frac{1}{2} \left(1 + \text{erf}\left(\frac{n}{\sqrt{2}}\right)\right)\right]\\ &= \text{erf}\left(\frac{n}{\sqrt{2}}\right). \end{align*} \end{split}\]

Show this for: generic normal distribution \(f\) with mean \(\mu\) and std \(\sigma\)

It is noted that in the case that \(\left|y\right|=n\sigma\),

\[ \text{Pr}\left(\mu - y \leq x \leq \mu + y\right) = \text{Pr}\left(\mu - n\sigma \leq x \leq \mu + n\sigma\right) = \text{erf}\left(\frac{n}{\sqrt{2}}\right). \]

So, for \(n=1\),

\[ \text{Pr}\left(\mu - \sigma \leq x \leq \mu + \sigma\right) = \text{erf}\left(\frac{1}{\sqrt{2}}\right) \]

However, at this point we are at an impass analytically, as the integral of a Gaussian function over a finite range has no analytical solution, and must be evaluated numerically.

import math
from scipy import special as special

def prob_n_sigma(n):
    return special.erf(n / math.sqrt(2.0))

prob_n_sigma(1)

\(p\)-values

Two-Tailed \(p\)-value

One-Tailed \(p\)-value

previous

Gaussian Sampling and use of Maximal Likliehood Estimators

next

The \(\chi^2\) Distribution