.ipynb .pdf

repository open issue suggest edit

Binder Colab

Contents

Matthew Feickert, October 2016

import numpy as np
import scipy.stats as stats
import scipy.optimize as optimize

import matplotlib.patches as mpatches
import matplotlib.pyplot as plt

Probability integral transform

The probability integral transform states that if $X$ is a continuous random variable with cumulative distribution function $F_X$, then the random variable ${\displaystyle Y=F_X(X)}$ has a uniform distribution on $[0,1]$. The inverse of this is the “inverse probability integral transform.’’ [1]

“Proof”

Let a random variable, $Y$, be defined by $Y={\displaystyle F_X(X)}$ where $X$ is another random variable. Then,

$$\begin{array}{r}\begin{array}{rl}{F}_Y(y)& =\text{P}(Y\le y)\\ & =\text{P}(F_X(X)\le y)\\ & =\text{P}(F_X(X)\le F_X^{-1}(y))\\ & =F_X(F_X^{-1}(y))\\ & =y.\end{array}\end{array}$$

${\displaystyle F_Y(y)=y}$ describes the cumulative distribution function of a random variable, i.e., $Y={\displaystyle F_X(X)}$, uniformly distributed on $[0,1]$. [1]

Alternative View: A Change of variables

Consider the variable transformation

$$y(x)=F(x)=\underset{-\mathrm{\infty }}{\overset{x}{\int }}f(x^{\prime })d{x}^{\prime }.$$

So the transofrmation from the distribution $f(x)$ to the distribution $f(y)$ required a Jacobian (determinant),

$$\begin{array}{r}\begin{array}{rl}\frac{dy}{dx}& =\frac{d}{dx}\underset{-\mathrm{\infty }}{\overset{x}{\int }}f(x^{\prime })d{x}^{\prime }\\ & =f(x),\end{array}\end{array}$$

such that the distribution of $y$ is

$$\begin{array}{r}\begin{array}{rl}f(y)& =\left(\frac{1}{\left|\frac{dy}{dx}\right|}\right)f(x)\\ & =\frac{f(x)}{f(x)}\\ & =1,\end{array}\end{array}$$

which is the probability density function for the Uniform distribution from $[0,1]$. [2]

Example:

Let’s uniformly sample $n$ measurements from a Gaussian distribution with true mean $\mu$ and true standard deviation $\sigma$.

x = np.linspace(-5.0, 5.0, num=10000)
# mean and standard deviation
mu = 0
sigma = 1

# sample the distribution
number_of_samples = 5000
samples = np.random.normal(mu, sigma, number_of_samples)
samples.sort()

# get sample parameters
sample_mean = np.mean(samples)
sample_std = np.std(samples)

true_distribution = stats.norm.pdf(x, mu, sigma)

Histogram the distribution

n_bins = 1
if number_of_samples < 50:
    n_bins = number_of_samples
else:
    n_bins = 50

# Plots
plt.figure(1)

# Plot histogram of samples
hist_count, bins, _ = plt.hist(
    samples, n_bins, density=True
)  # Norm to keep distribution in view
# Plot distribution using sample parameters
plt.plot(x, true_distribution, linewidth=2, color="black")

# Axes
plt.title("Plot of distribution from samples")
plt.xlabel("$x$")
plt.ylabel("count (normalized to unit area)")
sample_window_w = sample_std * 1.5
# plt.xlim([sample_mean - sample_window_w, sample_mean + sample_window_w])
plt.xlim([-4, 4])
plt.ylim([0, hist_count.max() * 1.6])

# Legends
sample_patch = mpatches.Patch(
    color="black", label=fr"distribution: $f(x;\mu={mu},\sigma={sigma})$"
)
data_patch = mpatches.Patch(
    color="blue",
    label=f"Histogram of {number_of_samples} samples of the distribution",
)

plt.legend(handles=[data_patch, sample_patch])

plt.show()
# print(samples)

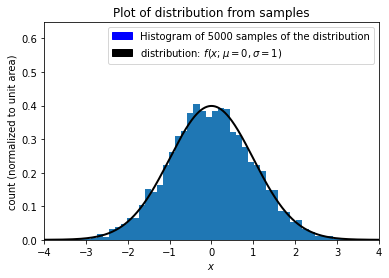
Now let’s feed our samples through the cumulative distribution function

# Plots
plt.figure(1)

# Plot distribution using sample parameters
plt.plot(x, stats.norm.cdf(x), linewidth=2, color="black")

# Axes
plt.title("cumulative distribution function for the Gaussian")
plt.xlabel("$x$")
plt.ylabel("$F(x)$")

plt.xlim([-5, 5])
plt.ylim([0, 1.1])

plt.show()

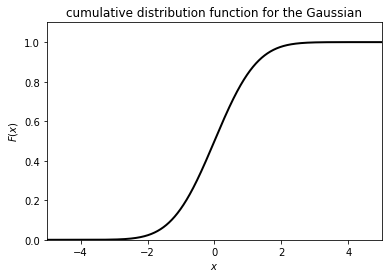
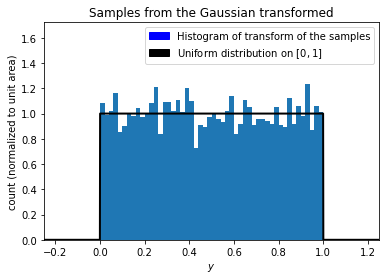
output = stats.norm.cdf(samples)
# print(output)

Now let’s plot the output and compare it to the uniform distribution.

# uniform distribution
uniform_distribution = stats.uniform.pdf(x)

# Plots
plt.figure(1)

# Plot histogram of samples
hist_count, bins, _ = plt.hist(
    output, n_bins, density=True
)  # Norm to keep distribution in view
# Plot distribution using sample parameters
plt.plot(x, uniform_distribution, linewidth=2, color="black")
# Axes
plt.title("Samples from the Gaussian transformed")
plt.xlabel("$y$")
plt.ylabel("count (normalized to unit area)")

plt.xlim([-0.25, 1.25])
plt.ylim([0, hist_count.max() * 1.4])

# Legends
sample_patch = mpatches.Patch(
    color="black", label=f"Uniform distribution on $[{0},{1}]$"
)
data_patch = mpatches.Patch(color="blue", label="Histogram of transform of the samples")

plt.legend(handles=[data_patch, sample_patch])

plt.show()

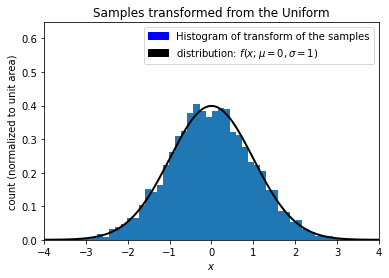
Now let’s use the quantile function to recover the original Gaussian distribution from the Uniform distribution.

recovered = stats.norm.ppf(output)

# Plots
plt.figure(1)

# Plot histogram of samples
hist_count, bins, _ = plt.hist(
    recovered, n_bins, density=True
)  # Norm to keep distribution in view
# Plot distribution using sample parameters
plt.plot(x, true_distribution, linewidth=2, color="black")
# Axes
plt.title("Samples transformed from the Uniform")
plt.xlabel("$x$")
plt.ylabel("count (normalized to unit area)")

plt.xlim([-4, 4])
plt.ylim([0, hist_count.max() * 1.6])

# Legends
sample_patch = mpatches.Patch(
    color="black", label=fr"distribution: $f(x;\mu={mu},\sigma={sigma})$"
)
data_patch = mpatches.Patch(color="blue", label="Histogram of transform of the samples")

plt.legend(handles=[data_patch, sample_patch])

plt.show()

Summary

Thus, we have seen that taking a distribution (pdf) $X$, and transforming it through the distribution’s cdf will result in an uniform distribution, $U$, and that transforming $U$ through the quantile function of $X$ will result in the pdf of $X$. Transformations back and forth between $X$ and $U$ by careful use of the properties of the cdf and quantile functions is a useful thing to think about. [3]

References

1. Wikipedia, Probability integral transform

2. K. Cranmer, “How do distributions transform under a change of variables?”

3. J. Hetherly, Discussions with the author while at CERN, October 2016

previous

The ${\chi }^2$ Distribution

next

Rejection Sampling